Основы электроники. ток, напряжение, сопротивление

Пару слов о BMS (Battery Management System)

Дело в том, что для того, чтобы управлять зарядом, предохранять от короткого замыкания и управлять силой выдаваемого тока к такой батарее надо приделать плату BMS (Battery Managment System). Самые простые выглядят вот так:

Чуть получше и дороже:

10S 36V на BMS говорит нам о том, что эта BMS рассчитана для 10 аккумуляторов, включенных последовательно. Если на каждом аккумуляторе будет по 3,6 В, следовательно, 10х3,6=36 Вольт что и написано на самой BMS.

Discharge current  — ток разрядки, то есть максимальный выдаваемый ток

Charge current — ток зарядки, то есть максимальный ток заряда

Внутри такой платы имеется все, чтобы полностью управлять состоянием батареи.

Схемы подключения таких BMS выглядят примерно вот так:

Как вы видите, у нас BMS вроде как должна заряжать только 10 банок в ряд. Но в нашей самопальной батарее их 40. Что же делать? Почему бы вместо одной банки не поставить в параллель 4 банки и не обмануть BMS?

Получается, схема с BMS 10s4p под плату с BMS будет выглядеть вот так:

В сообществе электронщиков и самоделкиных такая батарея называется 10S4P. Расшифровывается очень просто:

S — serial — с англ.  — последовательный.

P — parallel — параллельный.

В нашем случае 10 аккумуляторов последовательно и 4 в параллель — 10S4P. Все до боли просто)

А вот выглядит моя самопальная батарея для электровелосипеда пока что без модуля BMS.

Сила тока

Сразу возникает потребность в величине, которой мы будем «напор» электрического тока измерять. Такая, чтобы она зависела от количества частиц, которые протекают по проводнику.

Сила тока — это физическая величина, которая показывает, какой заряд прошел через проводник.

Сила тока измеряется в Амперах. Единица измерения выбрана не просто так.

Во-первых, она названа в честь физика Андре-Мари Ампера, который занимался изучением электрических явлений. А во-вторых, единица этой величины выбрана на основе явления взаимодействия двух проводников.

Здесь аналогии с водопроводом провести, увы, не получится. Шланги с водой не притягиваются и не отталкиваются вблизи друг друга (а жаль, было бы забавно).

Когда ток проходит по двум параллельным проводникам в одном направлении, проводники притягиваются. А когда в противоположном направлении (по этим же проводникам) — отталкиваются.

За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1 м, расположенные на расстоянии 1 м друг от друга в вакууме, взаимодействуют с силой 0,0000002 Н.

Задача

Найти силу тока в цепи, если за 2 секунды в ней проходит заряд, равный 300 мКл.

Решение:

Возьмем формулу силы тока

I = q/t

Подставим значения

I = 300 мКл / 2 с = 150 мА

Ответ: сила тока в цепи равна 150 мА

Закон Ома для полной цепи

Подробности

Просмотров: 432

«Физика — 10 класс»

Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?

Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.

В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.

Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).

Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: А_ст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому

А_ст = ΕIΔt.         (15.17)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:

Q = I2RΔt + I2rΔt.         (15.18)

По закону сохранения энергии А_ст = Q, откуда получаем

Ε = IR + 1r.         (15.19)

Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.

Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.

Закон Ома для замкнутой цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε

При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.

Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε₁, Ε₂, Ε₃ и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.

Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.

Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:

Ε_п = Ε₁ + Ε₂ + Ε₃ = lΕ₁| — |Ε₂| + |Ε₃|

Если Ε_п > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Ε_п < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи R_п равно сумме всех сопротивлений (см. рис. 15.11):

R_п = R + r₁ + r₂ + r₃.

Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):

I₁R₁+ I₂R₂ + … + I_nR_n = Ε₁ + Ε₂ + … + Ε_m

Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Параллельное соединение резисторов

Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.

При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:

1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:

1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.

R ≈ 1 / 0,164 ≈ 6,097 Ом.

Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):

Выделим основные особенности параллельного соединения резисторов:

• Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
• Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
• Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
• Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

В общем, это наиболее распространенные варианты использования этих соединений.

Закон ома для неоднородного участка цепи

Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.

Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.

Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.

На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.

Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.

Учитывая вышесказанное, можно установить следующую зависимость:

I = U/ R = (f1 – f2) + E/ R,

Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.

Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».

Последовательно-параллельное соединение источников питания

А кто вам мешает соединять аккумуляторы или батарейки сразу и последовательно и параллельно? Но разве так можно? Можно). На примере с водобашнями это может выглядеть вот так:

Здесь мы видим две башни, каждая из которых состоит их двух башенок, и эти две большие башни соединены с помощью трубы.

Очень часто последовательно-параллельное соединение используется в электротранспорте. Недавно я делал батарею для своего электровелосипеда из li-ion аккумуляторов 18650. Для моего электробайка требовалось напряжение в 36 Вольт. Итак, теперь включаем логику. Один аккумулятор выдает 3,6 Вольт. Чтобы получить 36 Вольт, мне надо соединить 10 аккумуляторов последовательно.

Чтобы было проще для понимания, я их нарисую не по ГОСТу:

Ура! Я получил 36 Вольт для своего электровелосипеда. Но вот проблема в том, что один такой аккумулятор может отдать в нагрузку силу тока 2800 миллиАмпер в течение 1 часа или 2,8 Ампер в течение 1 часа. Такой параметр указывается на аккумуляторах как mAh. Об этом я подробно писал в этой статье «Как измерить ток и напряжение мультиметром«.

То, что я все аккумуляторы соединил последовательно, не означает, что их емкость возросла в 10 раз. В 10 раз возросло только напряжение, так как я их соединил последовательно. То есть общая сумма получилась 36 Вольт и все те же самые 2800 mAh как и у одного аккумулятора.

Поэтому, чтобы увеличить емкость, я должен в параллель этой ветви соединить точно такую же ветвь из аккумуляторов, иначе мой электровелосипед не проедет и пару тройку километров. Я ведь хочу кататься весь день!

Сказано — сделано. Цепляем еще одну ветвь в 36 Вольт. Вы ведь не забыли правило, что при параллельном соединении у нас напряжение должно быть одинаково? В результате мы получаем что-то типа этого:

Итого, мы получили те же самые пресловутые 36 Вольт, но вот емкость увеличилась в два раза. 2800 mAh +2800 mAh = 5600 mAh. Ну вот, с такой батареей можно проехать уже чуть дальше. Но мне этого тоже показалось мало, поэтому я добавил еще 2 ветви. В результате моя самопальная батарея для электровелосипеда схематически, по идее, должна выглядеть вот так:

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

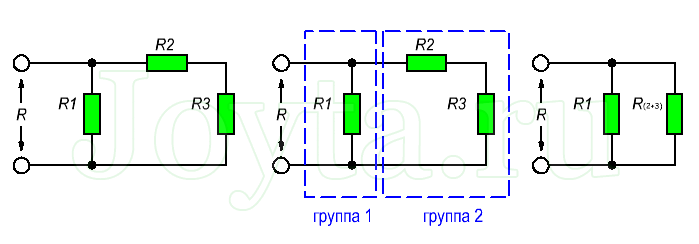
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

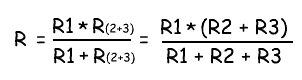
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Соединение резисторов — пример расчета

В качестве примера смешанного соединения резисторов рассмотрим систему распределения электроэнергии и систему заземления в частном доме. Несмотря на то, что данная схема отношения к электронике не имеет, а в качестве резисторов выступают контуры заземления, все же принципы одни и те же. К тому же, вместо того, чтобы рассматривать произвольную цепь, намного интересней и познавательней дополнительно разобраться в вопросах электричества в быту.

На приведенной выше схеме показана система распределения электроэнергии по системе TN-C-S. Слева направо:

• Источник питания U = 220 В (распределительный трансформатор) с глухозаземленной нейтралью R1 = 2 Ом.
• Далее R2 = 4000 Ом — это имитация прикосновения человека к зануленному корпусу, находящемуся в доме с системой заземления TN-C-S.
• R3 = 30 Ом — повторное заземление в доме с системой TN-C-S.
• R4 = 4 Ом — сопротивление контура заземления (система TT) в соседнем доме.

В доме с системой заземления TT смоделирован пробой фазы на корпус при неработающей автоматике отключения питания. Поэтому потенциал через землю направился к нейтрали трансформатора по трем путям (участок параллельного соединения):

• Через заземление 30 Ом соединенное с нейтралью (рабочий нулевой проводник).
• Через землю — пол — человека — зануленный прибор (4000 Ом).
• Через заземление нейтрали трансформатора 2 Ом.

Получаем параллельное соединение резисторов — R1, R2, R3, и последовательное соединение — R4 и группа с параллельным соединением.

Прежде чем переходить к расчету в цепи со смешанным соединением резисторов, отметим, о чем данная симуляция свидетельствует. Нельзя допускать в одной системе распределения электроэнергии наличия различных систем заземления. Так, согласно приведенной модели, при пробое фазы на корпус в системе TT произошел вынос опасного потенциала 70 В на корпус прибора в соседнем доме с системой заземления TN-C-S. Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.

Рассчитаем, на сколько снизится выносимый потенциал (напряжение), если добавить в участок с параллельным соединением еще 29 домов с системой заземления TN-C-S (сопротивление повторного заземления каждого дома 30 Ом).

Согласно методике расчета в первую очередь определим общее сопротивление на участке с параллельным соединением:

1 / R = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4 = 1 / 2 + 1 / 4000 + 1 / 30 + 29 / 30 = 1,5 Ом.

R = 1 / 1,5 = 0,67 Ом.

Теперь можно рассмотреть последовательное соединение с резисторами R123(+29 по 30 Ом) = 0,67 Ом и R4 = 4 Ом. R = R123(+29 по 30 Ом) + R4 = 4,67. Зная напряжение, находим силу тока:

I = U / R = 220 / (4 ,67) = 47,1 A.

Зная силу тока, найдем напряжение на участке с параллельным соединением резисторов (где общее сопротивление 0,67 Ом):

U123(+29 по 30 Ом) = R123(+29 по 30 Ом) × I = 0,67 × 47,1 = 31,5 В.

Как видно с добавлением в участок с параллельным соединением 29 дополнительных резисторов с сопротивлением каждого 30 Ом общее сопротивление и напряжение снизились. И, несмотря на то, что ток всей цепи возрос, ток проходящий через человека (R2 = 4000 Ом) значительно снизился за счет снижения напряжения участка цепи. Если посмотреть схему, то изначально через тело человека проходило 17,6 mA. После добавления 29 резисторов это значение снизилось: I2 = U123(+29 по 30 Ом) / R2 = 31,5 / 4000 = 0,0078 A = 7,8 mA.

Подведем итог. При различном соединении резисторов расчет их общих сопротивлений выполняется в соответствии с простыми формулами. И помимо изменения сопротивления в цепи, согласно закону Ома можно проанализировать также такие параметры, как сила тока и напряжение на различных участках.

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения. Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока

В общем, это наиболее распространенные варианты использования этих соединений.

Последовательное соединение элементов

Параллельное соединение резисторов

Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.

Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи. Последовательное включение резисторов

Последовательное включение резисторов

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:

I = U/R.

Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:

R = U/I.

Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.

Проходящий по цепи ток везде одинаковый:

I = I1= I2= … = In.

Прикладываемое напряжение является суммой напряжений на каждом резисторе:

U = U1 + U2+ … + Un.

Следовательно, рассчитать можно общее:

Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.

Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R

Отдельный участок и полная электрическая цепь

Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:

• Отдельный краткий участок. Является частью схемы без источника ЭДС.
• Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.

Расчет тока участка электрической схемы

В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:

Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.

Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.

Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.

В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.

Вариант расчета для полной цепи

Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.

С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.

Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.

Действие закона к переменной величине

При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.

Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.

Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.

Последовательное соединение источников питания

Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:

Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.

Если «минус» одной батарейки соединить с «плюсом» другой батарейки, то их общее напряжение суммируется.

Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос — это ЭДС.

Наполовину разряженная батарейка будет уже выглядеть примерно вот так:

Можно сказать, насос уже не справляется.

Батарейка посаженная в «ноль» будет выглядеть вот так:

Насос автоматической подачи воды сломался.

Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:

Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса — черный.

Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.

На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.

Таким же способом замеряем напряжение на аккумуляторе №2

О, как совпало). Те же самые 3,66 Вольт.

Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:

Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.

Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.

Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.

Похожие записи:

Фундамент из бутового камня Как и чем сделать отделку откосов окон снаружи Отделка бани Расчет минимального и оптимального угла наклона крыши в процентах и градусах в зависимости от вида крыши и кровельного материала Обои для кухни: 11 предрассудков, мифов и домыслов Баня по-черному своими руками: особенности постройки