Расчёт сопротивления проводника: определение и метод измерения

Цепь переменного тока

Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:

  • активным;
  • индуктивным;
  • емкостным;
  • полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).

Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.

Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.

При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:

  • w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
  • C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.

Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt . В ЦПТ величина Z зависит от:

  • геометрии П;
  • типа вещества, из которого сделан П;
  • температуры;
  • деформации различного вида;
  • электрических показателей I, U, f, L, C и R.

Зависимость удельного сопротивления от температуры

Говоря об удельном сопротивлении, нельзя упомянуть о влиянии температуры окружающей среды на его значение. Однако, это влияние будет разным для каждого материала. Это объясняется одним важным параметром $α$ — температурным коэффициентом.

Температурный коэффициент используется в формула для расчета удельного сопротивления с учетом изменения температуры:

$ρ_t =ρ_0 • $, где

  • $ρ_0$ — удельное сопротивление при 20 С*,
  • $α$ — температурный коэффициент,
  • $t-t_0$ — разница температур.

Рассчитаем удельное сопротивление меди при -30 C и +30 C .

Пример 1

Для расчета удельного сопротивления при +30 C*, нужно взять первую формулу и подставить известные значения:

$ρ_t=ρ_0 • =0,017• =0,017•=0,0176 $

Для расчета удельного сопротивления при -30 C*, нужно взять вторую формулу и выполнить аналогичный расчет:

$ρ_t=ρ_0 • =0,017 • [1+(0,0039 • (– 30 – 20)=0,0136$

Исходя из расчетов можно сделать вполне логичный вывод, который заключается в следующем.

Замечание 2

Чем выше температура окружающей среды, тем выше удельное сопротивление.

Измерение сопротивления

На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда » в эквивалентный «треугольник » и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

Пример из практики

Последовательно с источником освещения включен тестер. Напряжение осветительного прибора = 220 Вольт. Мощность неизвестна. На показателе амперметра указано 276 миллиампер тока. Какая величина у спирали лампы при последовательном включении в схему резисторов?

Формула нахождения сопротивления спирали

Электросопротивление представляет собой физическую величину, которая соответствует степени препятствия движению электрических частиц у каждого материала. Возможно измерить уровень величины мультиметром. В таком случае придется находить значение по формуле. Для предотвращения попадания электрического тока на непредназначенные для этого участки желательно заземлять линии передачи. Данная физическая величина используется во многих радиодеталях, например, светодиодах. В электрической цепи, чтобы узнать величину, требуется подключить к вольтметру фазу и ноль при известной силе тока, затем рассчитать по закону Ома.

Расчет сопротивления последовательных резисторов

Cила тока: формула

При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина. Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.

Как найти сопротивление формула для последовательной цепи

Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.


Резистор

Аналогия с электрическим сопротивлением проводника на примере резистора

Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.

Активное сопротивление

Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.

Реактивное сопротивление

К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.

Индуктивная нагрузка

Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:

Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Емкостная нагрузка

При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.

Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами

Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.

Как смотреть силу тока в цепи через осциллограф

Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:

На схеме мы видим генератор частоты и резистор.

Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты

А также цифровой осциллограф:

С помощью него мы будем смотреть напряжение и силу тока. 

Что?

Силу тока?

Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.

Кто не помнит —  напомню. Имеем обыкновенный резистор:

Что будет, если через него прогнать электрический ток?

На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах

И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на  самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉

Активные и реактивные сопротивления

Сопротивление нагрузки бывает активным и реактивным. Активное сопротивление (R) не зависит от частоты сети. Это означает, что ток в нем изменяется синхронно с напряжением. Это то сопротивление, которое мы измеряем мультиметром или тестером.

Обозначение активного сопротивления

Реактивное сопротивление делится на два вида:

— индуктивное (трансформаторы, дроссели);

— емкостное ( конденсаторы).

Обозначение емкостного сопротивления

Отличительная черта реактивной нагрузки – наличие опережения или отставания тока от напряжения. В емкостной нагрузке ток опережает напряжение, а в индуктивной – отстает от него. Физически это выглядит так: если разряженный конденсатор подключить к источнику постоянного тока, то в момент включения ток через него максимальный, а напряжение – минимальное. Со временем ток уменьшается, а напряжение — возрастает, пока конденсатор не зарядится. Если подключить конденсатор к источнику переменного тока, то он будет постоянно перезаряжаться с частотой сети, а ток — увеличиваться раньше, чем напряжение.

Подключив к источнику постоянного тока индуктивность, получим обратный результат: ток через нее будет нарастать некоторое время после подключения напряжения.

Величина реактивного сопротивления зависит от частоты. Емкостное сопротивление:

Угловая частота, связанна с частотой сети f формулой:

Как видно из формулы, при повышении частоты емкость уменьшается.

С Фарада (Ф) емкость
ѡ 1/с угловая частота
f Герц (Гц) частота
L Генри (Гн) индуктивность

Последовательное подключение

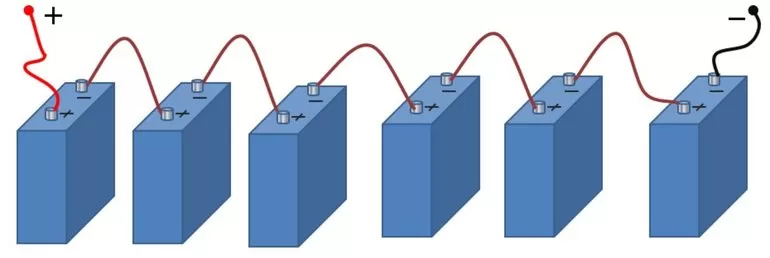
Для удобства при изображении разветвлённой электрической цепи все сопротивления чертят в виде прямоугольников, которые являются резисторами. У любого такого элемента можно выделить два вывода. Один является началом, а другой — концом. С учетом сказанного можно сформулировать определение для последовательного соединения проводников: подключение, при котором конец предыдущего элемента соединён с началом последующего, называют последовательным.

Любой проводник обладает электрическим сопротивлением. Целью преобразования является замена чередующейся последовательности одним резистором. При этом по своим электрическим свойствам он должен не отличаться от всей цепочки. Простыми словами это можно пояснить так: если взять два чёрных ящика, у которых есть по паре выводов, причём один будет содержать всю электроцепь, а другой быть её эквивалентом, то определить, в каком из них находится схема, а где эквивалент, будет невозможно.

При последовательном соединении происходят следующие явления. Пусть имеется прямая цепочка, содержащая n резисторов: R1 + R2 + … +Rn. Сила тока — это величина, которая равняется заряду, протекающему за единицу времени. Можно представить, что в первом резисторе значение электротока будет больше, чем во втором. В результате возникнет «пробка», и скорость движения зарядов замедлится.

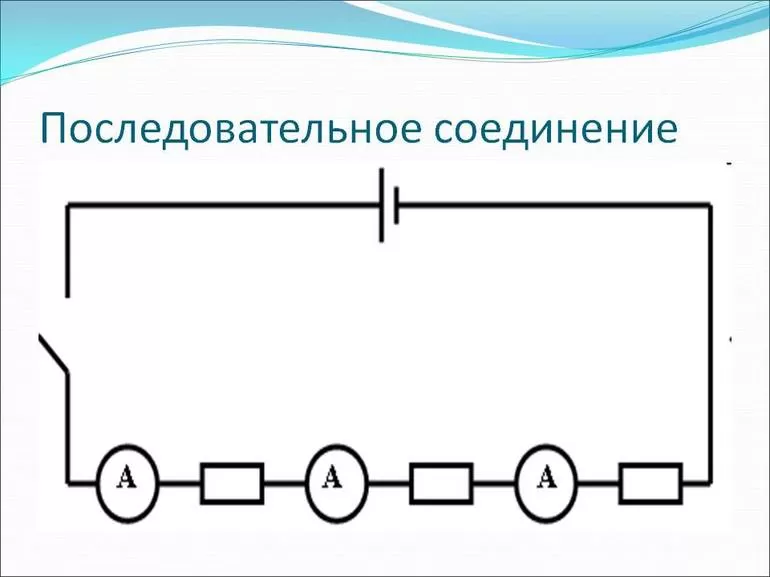
В точке соединения элементов произойдёт накопление электронов, что приведёт в ней к росту напряжения. Соответственно, сила тока на первом резисторе будет уменьшаться, а на втором, наоборот, увеличиваться. Это приведёт к выравниванию количества проходящих через резисторы зарядов, поэтому сила тока практически за мгновение во всей последовательной цепи станет одинаковой.

Напряжение — это работа, выполняемая по переносу заряда. По закону сохранения энергии общее её значение равняется их сумме на различных этапах. Общую разность потенциалов можно будет определить, сложив напряжения на каждом элементе. Такой вид подключения описывается следующими выражениями:

  • I = I 1 = I 2 = … = In;
  • U = U1 + U2 + … +Un.

Электродвижущая сила

Перемещение электронов в любом источнике создаётся с помощью сторонних сил. Их природа может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов. В генераторах тока они появляются как результат движения проводников в магнитном поле. Источник тока в электрической схеме играет ту же роль, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Вам это будет интересно Классификация воздушных и подземных ЛЭП и их назначение

Под воздействием внешних сил заряды двигаются внутри источника тока против сил электростатического поля. Это позволяет поддерживать постоянный ток в замкнутом контуре до тех пор, пока работают внешние силы. Физическая величина, равная отношению затраченной энергии сторонних сил на перемещение заряда, называется электродвижущей силой источника тока. Она может быть представлена формулой ℰ = A/q. В этом выражении:

  • ℰ — ЭДС в вольтах;
  • A — работа в джоулях;
  • q — заряд в кулонах.

По аналогии с замкнутой гидравлической системой и насосом, электрические заряды протекают непрерывно по всему контуру, и привести их в движение могут только внешние силы. Это означает, что работу по перемещению заряда любым источником можно рассматривать как ЭДС и измерять в вольтах. Вывод о модели цепи с источником, в которой протекает ток, как о замкнутом контуре крайне важен для понимания закона Ома для полного участка цепи.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению: на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны. С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC . Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC . Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов. U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² . Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

XL = ωL = 2πfL — реактивное сопротивление индуктивности. XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа, где действительной его частью является активное сопротивление, а мнимой — реактивное. Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:

Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ. В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:

Отсюда активная составляющая импеданса R = Zcosφ Реактивная составляющая X = Zsinφ.

Как определить формулой общее сопротивление цепи

Из закона Ома исходит то, что общее сопротивление равно общему напряжению, деленному на общую силу тока в цепи. При параллельном подключении напряжение, как уже было сказано, равно везде, поэтому необходимо узнать его значение на любом участке цепи. С током все сложнее, так как на каждой ветке его значение свое и зависит от конкретного R.

Также необходимо помнить, что могут быть параллельные подключения с нулевым значением R. Если в какой-либо ветке нет резистора или другого подобного элемента, но весь ток будет течь через нее и все общее значение для цепи станет нулевым. На практике это случается при выходе резистора из строя или при замыкании. Такая ситуация может навредить другим элементам из-за большой силы тока.

Таблица удельной величины для различных проводников

Влияние частоты тока на электроприборы

Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.

Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.

Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.

Источник

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

В общем, это наиболее распространенные варианты использования этих соединений.

Похожие записи:

Сварочный аппарат для полипропиленовых труб: топ-15 лучших аппаратов для пайки Односкатная крыша своими руками: устройство, конструкция, чертежи Установка встраиваемых в потолок колонок Укладка тротуарной плитки под автомобиль своими руками Красивые эффекты изображений для рисования на чпу плоттере Строительство дома из газобетонных блоков