Входное и выходное сопротивление

Связь с удельной проводимостью

В изотропных материалах связь между удельным сопротивлением ρ {displaystyle rho } и удельной проводимостью σ {displaystyle sigma } выражается равенством

ρ = 1 σ . {displaystyle rho ={frac {1}{sigma }}.}

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρ i j {displaystyle rho _{ij}} и тензора удельной проводимости σ i j {displaystyle sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:

J i ( r → ) = ∑ j = 1 3 σ i j ( r → ) E j ( r → ) . {displaystyle J_{i}({vec {r}})=sum _{j=1}^{3}sigma _{ij}({vec {r}})E_{j}({vec {r}}).}

Из этого равенства и приведённого ранее соотношения для E i ( r → ) {displaystyle E_{i}({vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:

ρ 11 = 1 det ( σ ) , {displaystyle rho _{11}={frac {1}{det(sigma )}},} ρ 12 = 1 det ( σ ) , {displaystyle rho _{12}={frac {1}{det(sigma )}},}

где det ( σ ) {displaystyle det(sigma )} — определитель матрицы, составленной из компонент тензора σ i j {displaystyle sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов.

Расчет сопротивления последовательных резисторов

Cила тока: формула

При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина. Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.

Как найти сопротивление формула для последовательной цепи

Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.

Резистор

Использование параметра внутреннего сопротивления при отработке технологии изготовления источников тока и диагностике их состояния

Измерения внутреннего сопротивления ХИТ
могут быть использованы разработчиками при
отработке технологии их изготовления. В этом
случае наиболее полезной является информация о сопротивлении R_Ω, так как она дает возможность лучше выявить все зависимости
между конструктивными и технологическими
параметрами и конечными характеристиками
изделия. Такая информация помогает быстрее
выбрать лучший сепарационный материал, определить допуски при дозировке электролита,
оценить плотность сборки.

Для диагностики технического состояния
ХИТ (степени разряженности, степени деградации, состояния после длительного хранения) в зависимости от природы источников
тока разных электрохимических систем полезной может быть информация и об омическом сопротивлении, и о поляризационном.

У герметичных источников тока с водным
электролитом (щелочных и свинцово-кислотных) осушение сепаратора в результате разбухания электродов и некоторых потерь воды,
изменение плотности сборки электродов и деформация аккумуляторов в результате повышенного давления приводят к увеличению
омического сопротивления. У литиевых источников тока этот эффект выражен меньше, а изменение поверхностной анодной пленки сказывается на поляризационном сопротивлении.

К сожалению, изменения параметров внутреннего сопротивления ХИТ в литературе обычно описывают только качественно.
Из-за большого спектра используемых в разных приложениях источников тока, разнообразия их конструкций и технологий изготовления диагностика состояния ХИТ по величине их внутреннего сопротивления может стать
возможной лишь при накоплении данных относительно конкретных источников тока ,
так как:

разброс R_Ω свежеизготовленных ХИТ конкретного типа может быть соизмерим с изменением RΩ этого источника тока в процессе разряда; это в наибольшей степени касается отечественных аккумуляторов;
разброс внутреннего сопротивления аккумуляторов ведущих зарубежных компаний, таких как SAFT, SANYO, PANASONIC, обычно не превышает 20%;
изменения R_Ω при изменении степени разряженности зависят от типа источника тока и его емкости;
изменения R_Ω при изменении степени разряженности и степени деградации различны у разных производителей;
диагностика литиевых источников тока по их внутреннему сопротивлению затруднена из-за быстрой пассивации анода, а разброс сопротивления пассивной пленки значительно увеличивается со временем хранения.

Возможности диагностирования состояния
литий-ионных аккумуляторов изучены плохо, но известно, что их омическое сопротивление в процессе разряда увеличивается мало,
а пассивация их анодов разного состава соизмерима с пассивацией металлического литиевого анода в литиевых элементах.

Из сказанного следует, что определение состояния источника тока с неизвестной предысторией эксплуатации весьма проблематично.
Однако при периодическом измерении R_Ω
ХИТ в процессе эксплуатации (при одинаковой высокой степени заряженности и температуре) можно прогнозировать его работоспособность. Обычно источники тока считаются работоспособными до тех пор, пока их
фактическая разрядная емкость С_раз не станет
менее 60–50% от номинальной емкости (С_н).
Зависимость С_раз и омического сопротивления в пределах этого периода эксплуатации
достаточно точно описывается эмпирическим
уравнением

С_раз R_Ω = const

Поэтому, измерив омическое сопротивление
R_Ω используемого источника тока в начале эксплуатации, при периодических последующих
его измерениях можно с достаточной точностью предсказывать реальную емкость ХИТ.
И эта процедура занимает всего несколько секунд. Измерения сопротивления возможны
и на работающих в буферном режиме батареях.

Выявление момента ускорения деградации
источников тока позволяет своевременно принять меры по восстановлению их работоспособности или замене.

По скорости изменения сопротивления в течение срока службы можно судить и о правильности условий эксплуатации.

Сравнение величин R_Ω аккумуляторов в составе батареи можно использовать для быстрого выявления «слабых». Деформация аккумуляторов или высыхание сепаратора приводит
к значительному увеличению сопротивления
относительно среднего его значения для всех
аккумуляторов батареи.

Закон Ома для всей цепи.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Вольтметр, подключенный к лампочке, показывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать бесконечно большим, а силу тока, текущего через вольтметр, равной нулю.

РЕШЕНИЕ.

Задача № 2.
Дана схема (рис. 6-11, а). Во сколько раз изменится сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л₂ вдвое больше сопротивления лампы Л₁, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л₁.

Задача № 3.
В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Найти силу тока короткого замыкания I_к.з.

Задача № 4.
Вольтметр, подключенный к полюсам источника тока при разомкнутой внешней цепи, показал U₁ = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U₂ = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить еще один такой же (рис. 6-12, б) ? Что покажет этот вольтметр, если второй резистор присоединить к первому параллельно (рис. 6-12, в)?

Задача № 5.
Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Построить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от внешнего сопротивления R.

Задача № 6.
Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I₁ = 3 А . Какую силу тока I₂ покажет этот амперметр, если его зашунтировать сопротивлением R_ш = 0,1 Ом?

Задача № 7.
Дана схема (рис. 6-16). Емкости конденсаторов С₁, С₂ и ЭДС источника тока ε известны. Известно также, что ток короткого замыкания I_к.з. этого источника в три раза превосходит ток I, текущий в этой цепи. Найти напряженности Е₁ и Е₂ полей в конденсаторах, если расстояния между их обкладками равны d.

Задача № 8.
Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Определить напряжения U₁ и U₂ на конденсаторах и заряды q₁ и q₂ этих конденсаторов.

Задача № 9.
Имеется N одинаковых источников тока, которые соединяют сначала последовательно, затем параллельно, подключая каждый раз к одному и тому же внешнему сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при этом изменяется напряжение на внешней части цепи?

Задача № 10.
Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит посередине прибора (рис. 6-21, а). Найти показания вольтметров U₁ и U₂, подключенных к потенциометру, если их сопротивления R₁= 6 кОм и R₂ = 4 кОм. Внутренним сопротивлением r источника тока пренебречь.

Задача № 11.
Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Найти силу тока I₂ в сопротивлении R₂.

Задача № 12.
Проволока из нихрома образует кольцо диаметром D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом такой же проволокой. Найти разность потенциалов φ_b – φ_а между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм2.

Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Выберите дальнейшие действия:

Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике.

Как правильно найти и посчитать формулой сопротивление цепи

Сперва следует разобрать понятия и формулы. Индуктивный тип считается так: XL= ωL, где L – индуктивность цепи, а ω – круговая частота переменного тока, равная 2πf (f – частота переменного тока). Чем больше частота сети, тем большим R для нее становится какая-либо катушка индуктивности.

Вам это будет интересно Как рассчитать индуктивность катушки

Емкостный тип можно рассчитать по формуле: Xc = 1/ ωC, где С – емкость радиоэлемента. Здесь все наоборот. Если происходит увеличение частоты, то сопротивляемость конденсатора напряжению уменьшается. Из этого исходит то, что для сети постоянного тока конденсатор – бесконечно большое R.

Высчитать характеристику можно и с помощи других величин

Но не только вид сопротивления и радиоэлементы, обеспечивающие его, влияют на общее значение цепи. Особую роль играет также и способ соединения элементов в электроцепь. Существует два варианта:

Последовательный;
Параллельный.

В последовательном подключении

Это самый простой тип для практического и теоретического рассмотрения. В нем элементы резисторного типа соединяются, очевидно, последовательно, образуя подобие «змейки» после чего электрическая цепь замыкается. Посчитать общее значение в таком случае довольно просто: требуется последовательно сложить все значения, выдаваемые каждым из резисторов. Например, если подключено 5 резисторов по 5 Ом каждый, то общий параметр будет равен 5 на 5 – 25 Ом.

Формула последовательной сети

В параллельном подключении

Немного сложнее все устроено в параллельных сетях. Если при последовательном способе току нужно пройти все резисторы, то тут он вправе выбрать любой. На самом деле он просто будет разделен между ними. Суть в том, что есть характеристика, схожая для всех радиоэлементов, например, величина в 5 Ом означает, что для нахождения общего R необходимо разделить его на количество всех подключенных резисторов: 5/5 = 1 Ом.

Важно! Из-за того, что напряжение на параллельных участках одинаково, а токи складываются, то есть сумма токов в участках равна неразветвленному току, то Rобщ будет высчитываться формуле: 1/R = 1/R1 + 1/R2 + … + 1/Rn. Формула параллельной сети. Формула параллельной сети

Формула параллельной сети

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

I = I1 = I2 ;
U = U1 + U2 ;
R = R1 + R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

I = I1 + I2 … ;
U = U1 = U2 … ;
1 / R = 1 / R1 + 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Закон Ома для полной цепи

Подробности: Просмотров: 432

«Физика — 10 класс»

Сформулируйте закон Ома для участка цепи.
Из каких элементов состоит электрическая цепь?
Для чего служит источник тока?

Рассмотрим простейшую полную (т. е. замкнутую) цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора сопротивлением R (рис. 15.10). Источник тока имеет ЭДС Ε и сопротивление r.

В генераторе r — это сопротивление обмоток, а в гальваническом элементе сопротивление раствора электролита и электродов.

Сопротивление источника называют внутренним сопротивлением в отличие от внешнего сопротивления R цепи.

Закон Ома для замкнутой цепи связывает силу тока в цепи, ЭДС и полное сопротивление цепи R + r. Эта связь может быть установлена теоретически, если использовать закон сохранения энергии и закон Джоуля—Ленца (15.14).

Пусть за время Δt через поперечное сечение проводника проходит электрический заряд Δq. Тогда работу сторонних сил при перемещении заряда Δq можно записать так: А_ст = ΕΔq. Согласно определению силы тока (15.1) Δq = IΔt. Поэтому

А_ст = ΕIΔt. (15.17)

При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых г и Я, выделяется некоторое количество теплоты. По закону Джоуля—Ленца оно равно:

Q = I2RΔt + I2rΔt. (15.18)

По закону сохранения энергии А_ст = Q, откуда получаем

Ε = IR + 1r. (15.19)

Произведение силы тока и сопротивления участка цепи называют падением напряжения на этом участке.

Таким образом, ЭДС равна сумме падений напряжения на внутреннем и внешнем участках замкнутой цепи.

Закон Ома для замкнутой цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к полному сопротивлению цепи.

Согласно этому закону сила тока в цепи зависит от трёх величин: ЭДС Ε сопротивлений R внешнего и г внутреннего участков цепи. Внутреннее сопротивление источника тока не оказывает заметного влияния на силу тока, если оно мало по сравнению с сопротивлением внешней части цепи (R >> r). При этом напряжение на зажимах источника примерно равно ЭДС: U = IR = Ε — Ir ≈ Ε

При коротком замыкании, когда R ≈ 0, сила тока в цепи и определяется именно внутренним сопротивлением источника и при электродвижущей силе в несколько вольт может оказаться очень большой, если r мало (например, у аккумулятора r ≈ 0,1 — 0,001 Ом). Провода могут расплавиться, а сам источник выйти из строя.

Если цепь содержит несколько последовательно соединённых элементов с ЭДС Ε₁, Ε₂, Ε₃ и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных элементов.

Для определения знака ЭДС любого источника нужно вначале условиться относительно выбора положительного направления обхода контура.
На рисунке (15.11) положительным (произвольно) считают направление обхода против часовой стрелки.

Если при обходе цепи данный источник стремится вызвать ток в направлении обхода, то его ЭДС считается положительной: Ε > 0. Сторонние силы внутри источника совершают при этом положительную работу.

Если же при обходе цепи данный источник вызывает ток против направления обхода цепи, то его ЭДС будет отрицательной: Ε < 0. Сторонние силы внутри источника совершают отрицательную работу. Так, для цепи, изображённой на рисунке 15.11, при обходе контура против часовой стрелки получаем следующее уравнение:

Ε_п = Ε₁ + Ε₂ + Ε₃ = lΕ₁| — |Ε₂| + |Ε₃|

Если Ε_п > 0, то согласно формуле (15.20) сила тока I > 0, т. е. направление тока совпадает с выбранным направлением обхода контура. При Ε_п < 0, наоборот, направление тока противоположно выбранному направлению обхода контура. Полное сопротивление цепи R_п равно сумме всех сопротивлений (см. рис. 15.11):

R_п = R + r₁ + r₂ + r₃.

Для любого замкнутого участка цепи, содержащего несколько источников токов, справедливо следующее правило: алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС на этом участке (второе правило Кирхгофа):

I₁R₁+ I₂R₂ + … + I_nR_n = Ε₁ + Ε₂ + … + Ε_m

Следующая страница «Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Закон Ома для участка цепи

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

I = U/R

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

U = IR

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

R = U/I

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R.Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Предлагается простой Онлайн-калькулятор для практических расчётов.Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.После сброса ввести два любых известных параметра.

I=U/R; U=IR; R=U/I; P=UI P=U²/R; P=I²R; R=U²/P; R=P/I² U=√(PR) I= √(P/R)

U = V

R = Ω

I = A

P = W

Формула

Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.

Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.

Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.

Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.

Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:

олово — 9,9 * 10-8 Ом * мм2/м;
медь — 0,01724 Ом * мм2/м;
алюминий — 0,0262 Ом * мм 2/м;
железо — 0,098 * Ом * мм2/м;
золото — 0,023 Ом * мм2/м.

Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.

Параллельное соединение резисторов

При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.

Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.

Первые попытки

Первые попытки «накопить электричество» для дальнейшего его исследования и использования были предприняты в Голландии. Немец Эвальд Юрген фон Клейст и голландец Питер ван Мушенбрук, проводившие свои исследования в городке Лейден, создали первый в мире конденсатор, названный позже «лейденской банкой».

Накопление электрического заряда уже проходило под действием механического трения. Использовать разряд через проводник можно было в течение некоторого, достаточно короткого, промежутка времени.

Победа человеческого разума над такой эфемерной субстанцией, как электричество, оказалась революционной.

К сожалению, разряд (электрический ток, создаваемый конденсатором) длился настолько коротко, что создать постоянный ток не мог. Кроме того, напряжение, даваемое конденсатором, постепенно понижается, что не оставляет возможности получать длительный ток.

Нужно было искать иной способ.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

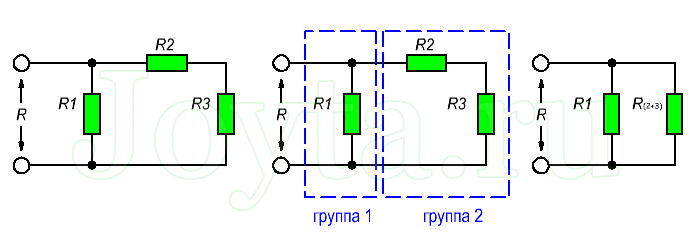
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Физические принципы[ | ]

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя

так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффектынеэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Внутреннее сопротивление невозможно убрать из двухполюсника
Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.

Что такое резистор и для чего он нужен

Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.

Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.

Для чего нужны резисторы: для подстройки параметров питания

Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.

Так выглядят переменные и постоянные резисторы

Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.

Как справиться с внутренним сопротивлением

Вот что советует писатель и эксперт по продуктивности Марк Макгинесс в своей книге «Мотивация для творческих людей».

Поймите, что от сопротивления нельзя избавиться

Оно похоже на хитрое многоголовое чудище, которое невозможно победить: стоит отрубить одну голову — сразу вылезет другая. Придётся признать, что сопротивление — наша неотъемлемая часть, и как‑то с ним уживаться.

Научитесь распознавать врага

Если вы не можете взяться за какое‑то дело, не ругайте себя за лентяйство. Напомните себе, что это сопротивление, и наблюдайте, какие формы оно принимает, чтобы в следующий раз узнать его безошибочно.

Оцените ущерб

Ответьте себе на вопрос: чего вы лишаетесь, если поддаётесь сопротивлению? Что вы теряете, если отказываетесь делать то, что для вас важно: меняться, учиться, пробовать новое, идти на риск? Запишите ответы. Скорее всего, в этом списке будут карьера и хороший заработок, интересные знакомства, любовь и отношения, здоровье, удовольствие от жизни, уверенность в себе и другие крайне приятные штуки

Понимание того, что всё это от вас ускользает, очень отрезвляет и мотивирует.

Включите режим профессионала

То есть относитесь к любой задаче отстранённо и по‑деловому. Представьте, что вы крутой специалист, для которого ваши трудности просто рутина, не вызывающая ни страха, ни сопротивления. «Подумаешь, большой и сложный проект на работе. Для меня это обычное дело, я прекрасно с ним справлюсь».

Упростите себе выбор

Чётко и детально планируйте своё время. Если вы подробно распишете все задачи, вам не придётся раздумывать, чем заняться, и будет меньше шансов увильнуть от каких‑то дел.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

заменяются участки провода, не отвечающие требованиям по диаметру сечения;
перекручиваются болтовые соединения с обязательной установкой врезных шайб;
вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
при необходимости в контур защитного заземления добавляются дополнительные элементы;
исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Проверка сопротивления петли «фаза – ноль»